1382 - 喷水装置
长 L 米,宽 W 米的草坪里装有 n 个浇灌喷头。每个喷头都装在草坪中心线上(离两边各 W/2 米)。
我们知道每个喷头的位置(离草坪中心线左端的距离),以及它能覆盖到的浇灌范围。
请问:如果要同时浇灌整块草坪,最少需要打开多少个喷头?
输入
输入包含若干组测试数据。
第一行一个整数 T 表示数据组数;
每组数据的第一行是整数 n、L 和 W ;
接下来的 n 行,每行包含两个整数,给出一个喷头的位置和浇灌半径。
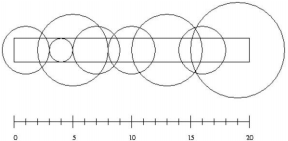
(上面的示意图是样例输入第一组数据所描述的情况)
输出
对每组测试数据输出一个数字,表示要浇灌整块草坪所需喷头数目的最小值。
如果所有喷头都打开也不能浇灌整块草坪,则输出 -1 。
样例
输入
3 8 20 2 5 3 4 1 1 2 7 2 10 2 13 3 16 2 19 4 3 10 1 3 5 9 3 6 1 3 10 1 5 3 1 1 9 1
输出
6 2 -1
提示
对于 100% 的数据,n <= 15000 。
#include<iostream>
#include<cmath>
#include<algorithm>
using namespace std;
struct asdf
{
int x1,r1;
double a,b;
}s[15005];
bool cmp(asdf aa , asdf bb)
{
return aa.a < bb.a;
}
int main()
{
int p;
int n,l,w;
int x,r;
int k,o;
cin>>p;
for(int pp=1 ; pp<=p ; pp++)
{
k=0;
o=0;//总次数
cin>>n>>l>>w;
for(int q=1 ; q<=n ; q++)
{
cin>>x>>r;
if(2*r > w)
{
s[++k].x1=x;
s[k].r1=r;
s[k].a=x-sqrt(r*r-pow(w/2,2));
s[k].b=x+sqrt(r*r-pow(w/2,2));
}
}
sort(s+1,s+1+k,cmp);
if(s[1].a > 0)
{
cout<<"-1"<<endl;
continue;
}
int v,e=1;//里循环,外循环
int vv=0;//起点
int yy;
while(s[e].b < l)
{
if(s[e].a <= vv)
{
v=1;
yy=0;
while(s[v].a <= vv)
{
if(s[v].b > yy)
{
yy=s[v].b;
}
v++;
}
vv=yy;
o++;
e++;
}
else
{
cout<<"-1"<<endl;
break;
}
}
cout<<o<<endl;
}
return 0;
}
来源
奇遇编程