3016 - 摆放花朵

某花店现有 F 束花，每一束花的品种都不一样。至少有同样数量的花瓶，被按顺序摆成一行。花瓶的位置是固定的，从左到右按 1\sim V 顺序编号，V 是花瓶的数目。

花束可以移动，并且每束花用 1\sim F 的整数标识。所有花束在放入花瓶时必须保持其标识数的顺序。例如，假设杜鹃花的标识数为 1，秋海棠的标识数为 2，康乃馨的标识数为 3，即杜鹃花必须放在秋海棠左边的花瓶中，秋海棠必须放在康乃馨左边的花瓶中。每个花瓶只能放一束花。

每个花瓶的形状和颜色也不相同，因此，当各个花瓶中放入不同的花束时，会产生不同的美学效果，并以美学值（一个整数 a i,j）来表示，空置花瓶的美学值为 0。在上述的例子中，花瓶与花束的不同搭配所具有的美学值，可以用如下的表格来表示：

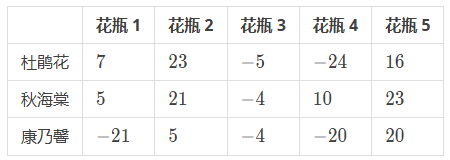
根据表格，杜鹃花放在花瓶 2 中，会显得非常好看，但若放在花瓶 4 中，则显得很难看。

为了取得最佳的美学效果，必须在保持花束顺序的前提下，使花的摆放取得最大的美学值，如果具有最大美学值的摆放方式不止一种，则输出每束花都尽量靠前的一种方案（即每束花所在的花瓶编号尽量小）。

输入文件的第一行是两个整数 F 和 V，分别为花束数和花瓶数。

接下来是矩阵 a i,j，共 F 行，每行 V 个整数，a i,j 表示花束 i 摆放在花瓶 j 中的美学值。

输出文件的第一行是一个整数，为最大的美学值；接下来一行 F 个整数，为那束花放入那个花瓶的编号。